가설검정
모집단과 표본
- 모집단: 연구 대상이 되는 전체 집단
- 표본: 모집단의 일부
귀무가설과 대립가설
- 귀무가설: 기존에 알려진 사실, 효과나 차이가 없음
ex) 퇴근후딴짓 강의 수강생과 타 강의 수강생과 합격률 차이가 없다
- 대립가설: 연구자가 입증하려는 사실, 효과나 차이가 있음
ex) 퇴근후딴짓 강의 수강생은 타 강의 수강생보다 합격률이 높다.
검정 결과
- 검정 통계량: 주어진 데이터와 귀무가설 간의 차이를 통계적으로 나타내는 값
- p-value(유의수준 0.05)
- 유의수준보다 작으면 귀무가설을 기각하고, 대립가설을 채택
- 유의수준보다 크면 귀무가설을 채택
가설검정 프로세스
- 통계적 가설 설정: 귀무가설과 대립가설
- 유의수준 결정: ex)0.05
- 검정 통계량 및 p-value(유의확률) 계산
- 결과 도출
t-test(t-검정)
| 단일표본검정 | 모집단 1개 | 한 그룹 | ex) 과자의 무게는 200g과 다른지 검정 |
| 대응(쌍체)표본검정 | 모집단 2개(같은 집단) | 같은 그룹 | ex) 신약 효과(전후) 검정 |
| 독립표본검정 | 모집단 2개 | 다른 그룹 | ex) 1반과 2반의 성적 차이 검정 |



범주형 데이터 분석(카이제곱 검정)
적합도 검정
- 관찰도수와 기대도수의 차이
- 빈도(count)로 변경(관찰값, 기대값)
# 적합도 검정
import scipy from stats
- stats.chisquare(observed, expected)
observed: 관찰된 빈도 리스트
expected: 기대 빈도 리스트
독립성 검정
- 두 변수가 서로 독립적인지(연관성이 있는지) 확인
- 교차표 테이블로 만들기
- 문제에서 표로 주어졌을 때
- 로우(원) 데이터가 주어졌을 때 -> pd.crosstab() 함수로 테이블 만들기
# 독립성 검정, 동질성 검정
import scipy from stats
- stats.chi2_contingency(table, correction = True)
- table: 교차표
- correction: 연속성 보정 (기본값 True)
동질성 검정
- 두 개 이상의 집단에서 동질성을 갖는지 확인
- 검정 절차는 독립성과 같음
분산분석
분석분석(ANOVA)은 여러 집단의 평균 차이를 통계적으로 유의미한지 검정
- 일원 일산 분석: 하나의 요인의 따라 평균의 차이 검정
- 이원 분산 분석: 두개의 요인의 따라 평균의 차이 검정
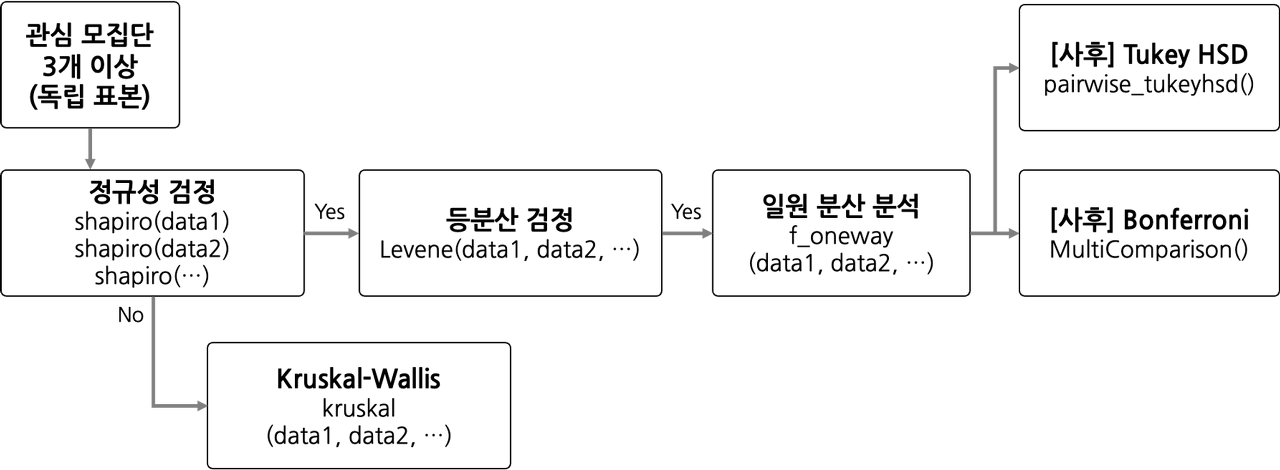
일원 분산분석
- 3개 이상의 집단 간의 평균의 차이가 통계적으로 유의한지 검정
- 하나의 요인이고, 집단의 수가 3개 이상일 때 사용
기본가정
독립성: 각 집단의 곽측치는 독립적이다.
정규성: 각 집단은 정규분포를 따른다. (샤피로 검정)
등분산성: 모든 집단은 동일한 분산을 가진다. (레빈 검정)
귀무가설과 대립가설
- 귀무가설: 모든 집단의 평균은 같다
- 대립가설: 적어도 한 집단은 평균이 다르다.
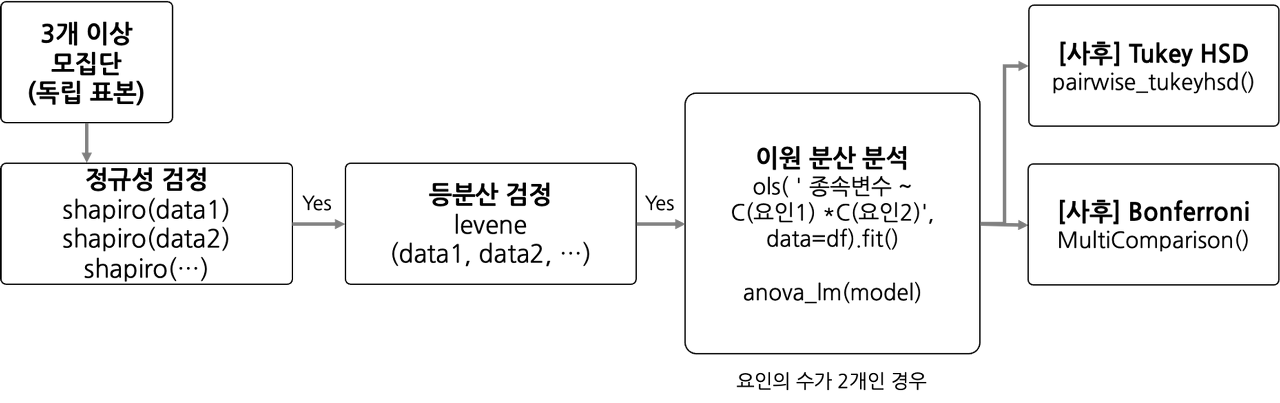
이원 분산 분석
- 3개 이상의 잡단 간의 평균의 차이가 통계적으로 유의한지 검정
- 요인의 수가 2개, 집단의 수가 3개 이상일 때 사용
기본가정
독립성: 각 집단의 곽측치는 독립적이다.
정규성: 각 집단은 정규분포를 따른다. (샤피로 검정)
등분산성: 모든 집단은 동일한 분산을 가진다. (레빈 검정)
귀무가설과 대립가설
주 효과(요인1)
- 귀무가설: 모든 그룹의 첫 번째 요인의 평균은 동일하다.
- 대립가설: 적어도 두 그룹은 첫 번째 요인의 평균은 다르다.
주 효과(요인2)
- 귀무가설: 모든 그룹의 첫 번째 요인의 평균은 동일하다.
- 대립가설: 적어도 두 그룹은 두 번째 요인의 평균은 다르다.
상호작용효과
- 귀무가설: 두 요인의 그룹 간의 상호작용은 없다.
- 대립가설: 두 요인의 그룹 간의 상호작용은 있다.
'[Python]' 카테고리의 다른 글
| [Python] 빅데이터분석기사 실기 연습(작업형3) (0) | 2023.10.30 |
|---|---|
| [Python] 빅데이터분석기사 실기 연습(작업형2) (0) | 2023.10.18 |
| [Python] 빅데이터분석기사 실기 연습(작업형1) (0) | 2023.10.18 |
| [Python] 통계 기본 정리 (0) | 2023.04.03 |
| [Python] pandas 기본 (0) | 2023.03.09 |